机器学习还是蛮有意思的啦，慢慢看，好好理解！

D2L

填充(padding)与步幅(stride)

image-20201123091439236

一般来说，在上下一共填充 $P_h$ 行，在左右一共填充$P_w$行，输出形状是：

$$
(n_h-k_h+p_h+1)\times(n_w-k_w+p_w+1)
$$
设施$p_h=k_h-1$和$p_w=k_w-1$可以使得输入和输出有着相同的形状。

2.2

2.22 带我毕设的学姐出去了。。。要好久

x = torch.zeros(5,3,dtype=torch.long,device= ,requires_grad=)这样的指定大小张量创建方式是最完整的。

重点：我们可以用 shape 或者size()来获得Tensor 的形状:

1
2
3
print(x.size())
print(x.shape)
输出：torch.Size([5,3])

返回的torch.Size其实是一个tuple

inplace版本数据操作

pytorch操作的inplace版本都有后缀，add_(x)等。

我们平时看到的 nn.ReLU(inplace=True)、nn.LeakyReLU(inplace=True)，这些语句中的inplace是什么意思？

  • inplace=True指的是进行原地操作，选择进行原地覆盖运算。 比如 x+=1则是对原值x进行操作，然后将得到的结果又直接覆盖该值。y=x+5,x=y则不是对x的原地操作。
  • inplace=True操作的好处就是可以节省运算内存，不用多储存其他无关变量。
  • 注意：当使用 inplace=True后，对于上层网络传递下来的tensor会直接进行修改，改变输入数据，具体意思如下面例子所示：
    Eg. inplace=True操作 会修改输入数据。
1
2
3
4
5
6
7
8
9
import torch
import torch.nn as nn
relu = nn.ReLU(inplace=True)
input = torch.randn(7)
print("输入数据：",input)

output = relu(input)
print("ReLU输出：", output)
print("ReLU处理后，输入数据：",input)

在这里插入图片描述

改变形状！这个经常用

用view()改变tensor的形状

1
2
3
4
y = x.view(15)
z = x.view(-1, 5) # -1的意思的其所指的维度可以根据其它维度推出来
print(x.size(), y.size(), z.size())
# torch.Size([5, 3]) torch.Size([15]) torch.Size([3, 5])

顾名思义，view仅仅是改变了对这个张量的观察⻆度，即更改其中一个，另外一个也会跟着改变。

如果一定要得到一个副本再改变其形状，则需要先clone()一下，再使用view()，使用clone的另一个好处是会被记录在计算图中，即梯度会传回副本时也会传给源tensor。

tensor和numpy互相转化

共享内存方式：numpy() from_numpy()`，数组共享相同的内存（所以他们之间的转换很快），改变其中⼀一个时另⼀一个也会改变！！！

拷贝创建式：torch.tensor()。

tensor在GPU上

用方法to()可以实现数据的移动。

1
2
3
4
5
6
7
8
if torch.cuda.is_available():
	device = torch.device("cuda") # GPU
	y = torch.ones_like(x, device=device) # 直接在GPU上创建tensor

    x = x.to(device) # 等价于 .to("cuda")
    z = x + y
    print(z)
    print(z.to("cpu", torch.double)) # to()还可以同时改变数据类型

2.3 自动求梯度

3.2 线性回归 从零开始实现（很重要！）

咱们直接伴随着代码将思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import torch
from matplotlib import pyplot as plt
from IPython import display
import numpy as np
import random

from d2lzh_pytorch import set_figsize

num_inputs = 2
num_examples = 100
true_w = [2, -3.4]#原始的参数
true_b = 4.2  #偏差bias
features=torch.from_numpy(np.random.normal(0,1,(num_examples,num_inputs)))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
'''这一段需要仔细体会！feature是1000行2列的向量， true_w[0] * features[:, 0]代表将1000个样本数据的第一个
参数基于真实的参数随机化，并且最后结果label是1000×1的向量'''

labels += torch.from_numpy(np.random.normal(0, 0.01, size=labels.size()))

# print(features[0], labels[0])
#问题https://blog.csdn.net/zl1107604962/article/details/101051338

# set_figsize()
# plt.scatter(features[:,1].numpy(),labels.numpy(),1)
# plt.show()

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices) # 随机读取
    for i in range(0, num_examples, batch_size):
        j = torch.LongTensor(indices[i: min(i + batch_size,num_examples)]) # 􀹋􀝸􀓞􀽺􀝢􁚆􀓧􁪃􀓞􀓻batch
        yield features.index_select(0, j), labels.index_select(0, j)
        #yield这里是生成器的用法，节约内存的写法

batch_size = 10
# for X, y in data_iter(batch_size, features, labels):
#     print(X, y)
#     break

w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
#初始化模型参数，这里随机初始化
b = torch.zeros(1, dtype=torch.float32)
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

def linreg(X, w, b):  #线性回归方程的矢量表示
    # b = torch.tensor(b, dtype=torch.float32)
    # w = torch.tensor(w, dtype=torch.float32)
    # X = torch.tensor(X, dtype=torch.float32)
    b = b.float()
    w = w.float()
    X = X.float()#更新后torch的写法
    return torch.mm(X, w) + b

def squared_loss(y_hat, y):#改变下实际中y的值，变得和y_hat一样
    # print("y_hat=",y_hat,"y=",y)
    return (y_hat - y.view(y_hat.size()))** 2 / 2

def sgd(params, lr, batch_size):#随机梯度下降法
    for param in params:
        param.data -= lr * param.grad / batch_size#用批量样本梯度平均值来看作梯度
		#我们传入的params都是有携带梯度的，backward()反向传播是根据损失函数把梯度更新了，
        #sgd这里做的是更新参数


lr = 0.03  #超参数，学习率
num_epochs = 3  #超参数，迭代次数
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()#正向传播算损失
        l.backward()#根据得到的损失反向传播
        sgd([w, b], lr, batch_size)#根据反向传播的梯度，更新参数
        
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d,loss %f'%(epoch+1,train_l.mean().item()))

3.3 利用pytorch实现线性回归

我觉得，在机器学习代码的编写中，网络结构的设计固然重要，但是在实现层面上，各种数据处理啊，维度啊，切片啊，又是很复杂需要时间的，因此在看人家源码的时候，一定有必要看懂别人数据处理部分的代码。

TensorDataset和DataLoader

TensorDataset 可以用来对 tensor 进行打包，就好像 python 中的 zip 功能。

1
2
3
4
5
6
7
8
9
10
a = torch.tensor([[1,2],[1,3],[1,4],[1,5],[1,6]])
b = torch.tensor([1,1,1,0,0])
c = Data.TensorDataset(a,b)
for x,y in c:
    print(x,y)
tensor([1, 2]) tensor(1)
tensor([1, 3]) tensor(1)
tensor([1, 4]) tensor(1)
tensor([1, 5]) tensor(0)
tensor([1, 6]) tensor(0)

DataLoader则是分批次输出：

1
2
3
4
5
6
7
8
train_loader = Data.DataLoader(c,batch_size=2,shuffle=True)
for i,data in enumerate(train_loader):
    x,y = data
    print("batch:%d"%i,x,y)
    
batch:0 tensor([[1, 3],[1, 2]]) tensor([1, 1])
batch:1 tensor([[1, 5],[1, 6]]) tensor([0, 0])
batch:2 tensor([[1, 4]]) tensor([1])

这样一次就能取batch_size个数据了，并且data为一个列表，label为一个列表。

最终结果是为了分批次打包成 data ：label的样子。

weight和bias的解释

在模型初始化的时候，会使用init.normal_来初始化，我一开始并不理解这个weight和bias是什么东西，看到我所初始化的Linear层有这两个参数，还以为是全连接层特有的，后面才发现，卷积啊其它的网络层都有这两个东西，那么它们到底是啥？且看这幅图片：

$o=w_1x_1+w_2x_2+b$

w和b不只是这个线性函数的的参数，而是输入层的细胞到下一层细胞的权重，只不过这里线性回归的网络太简单了，每个细胞没有再激活函数。

权重 weights

（w1，w2w3）是每个输入信号的权重值，以上面的（1x2x3）的例子来说，x1的权重可能是092，x2的权重可能是02，x3的权重可能是0.03。当然权重值相加之后可以不是1。

偏移 bias

还有个b是干吗的?一般的书或者博客上会告诉你那是因为Sy=wx+bs，b是偏移值，使得直线能够沿v轴上下移动。这是用结果来解释原因，并非b存在的真实原因。从生物学上解释，在脑神经细胞中，一定是输入信号的电平/电流大于某个临界值时，神经元细胞才会处于兴奋状态，这个b实际就是那个临界值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
from pyexpat import features
import torch
from matplotlib import pyplot as plt
from IPython import display
import numpy as np
import torch.utils.data as Data 
from torch import nn, optim
from d2lzh_pytorch import set_figsize


num_inputs = 2
num_examples = 1000
true_w = [5, 3]
true_b = 3.7

features = torch.tensor(np.random.normal(0,1,(num_examples,num_inputs)), dtype=torch.float)

labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b
labels += torch.tensor(np.random.normal(0,0.01, size=labels.size()), dtype = torch.float)

batch_size = 10
dataset = Data.TensorDataset(features, labels)
#(tensor([0.1116, 1.1318], dtype=torch.float64), tensor(7.6449, dtype=torch.float64))
data_iter = Data.DataLoader(dataset, batch_size,shuffle=True)

class LinearNet(nn.Module):
    def __init__(self, n_feature) -> None:
        super(LinearNet, self).__init__()
        self.linear = nn.Linear(n_feature, 1)
    #前向传播
    def forward(self, x):
        y = self.linear(x)
        return y

net = LinearNet(num_inputs)

# net = nn.Sequential(
#     nn.Linear(num_inputs, 1)
# )
#一般更常见的是sequential，但是哦我们也要熟悉使用各种不同方法来创建，在未来说不定可以专门写一个，来总结各种不同的创建网络的方法，和他们不同之处的对比。

nn.init.normal_(net.linear.weight, mean=0, std=0.01)#normal是正态随机初始化
nn.init.constant_(net.linear.bias, val=0)#constant就是直接设置参数了
loss = nn.MSELoss()
optimizer = optim.SGD(net.parameters(), lr = 0.03)

num_epochs = 6
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:#看懂前面数据产生和初始化就很容易知道这里在干什么了
        output = net(X)
        l = loss(output, y.view(-1,1))
        optimizer.zero_grad()
        l.backward()
        optimizer.step()
    print('epoch %d, loss %f '% (epoch, l.item()))

dense = net.linear
print(true_w, dense.weight)
print(true_b, dense.bias)

在整个示例代码中，有几个点需要注意记住下：

  • 在feature初始化的时候，注意方式的不同带来的数据格式的不同，他们会影响后面数据处理的函数使用：

    1
    2
    features=torch.from_numpy(np.random.normal(0,1,(num_examples,num_inputs)))
    features = torch.tensor(np.random.normal(0,1,(num_examples,num_inputs)), dtype=torch.float)

  • 在使用这种方法建立网络net之后，要得到其中某个网络层的参数：应该使用net.linear而不是net[0]。

卷积神经网络

3.9中的操作：其实就是把$28\times28$的图像展开成长为784的向量，输入全连接层之中。

局限性： 1.消耗内存 2.本来相邻的像素，现在却距离很远。

LeNet

  • 卷积层：识别图像的空间模式，线条+物体局部

  • 池化：降低敏感性

池化的窗口大小和步幅一样,这样池化不会重叠

这一部分代码没有什么特殊的，就是在实现每个网络，我认为这一部分是理解Pytorch的很好的例子，在经历前面的基础之后，利用这个图和网络代码的结构，可以很好的理解

一个有意思的想法：

AlexNet

网络结构：

  • 第一层 11×11的卷积：使用更大的框去捕获物体
  • 第二层 5×5 卷积，后面卷积全部用3×3
  • 第一、二、五卷积之后使用3×3，步幅为2的MAX池化
  • 两个输出个数4096的全连接层

特点：

  • sigmoid->ReLU，化简（梯度恒为1，能够持续有效训练）
  • 丢弃法控制复杂度
  • 图像增广，扩大数据集

VGG

核心思想：使用小的卷积层级联能够取得和大的卷积窗口同样的效果

如3个3×3代替一个7×7，2个3×3代替5×5，==能够在保证有相同感受野的情况下，提升了网络深度==

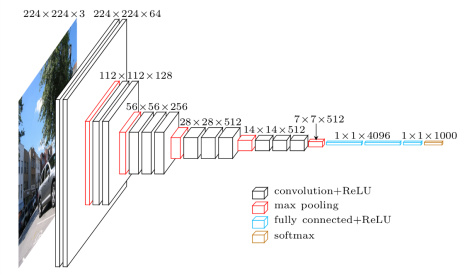
一文读懂VGG网络

高和宽逐渐减半，而通道数每次翻倍，最后7×7×512的层传入全连接层。

1
nn.MaxPool2d(kernel_size=2, stride=2)#这样的池化层会使得宽和高减半

一个小技巧：

下面构造一个高宽为224的单通道数据样本观察每一层的输出形状：

1
2
3
4
5
6
7
8
9
10
11
net = vgg(conv_arch, fc_features, fc_hidden_units)
X = torch.rand(1, 1, 224, 224)

for name, blk in net.named_children():
    X = blk(X)
    print(name,'输出形状：',X.shape)
    
vgg_block1 输出形状： torch.Size([1, 64, 112, 112]) 
vgg_block2 输出形状： torch.Size([1, 128, 56, 56])       
vgg_block4 输出形状： torch.Size([1, 512, 14, 14])       
vgg_block5 输出形状： torch.Size([1, 512, 7, 7])

其中named_children获取的是一级子模块及其名字，而named_modules返回所有的子模块，包括子模块的子模块

简单版的VGG：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
Sequential(
  (vgg_block1): Sequential(
    (0): Conv2d(1, 8, kernel_size=(3, 3), stride=(1, 1), 
padding=(1, 1))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (vgg_block2): Sequential(
    (0): Conv2d(8, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (vgg_block3): Sequential(
    (0): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): ReLU()
    (2): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (3): ReLU()
    (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (vgg_block4): Sequential(
    (0): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): ReLU()
    (2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (3): ReLU()
    (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (vgg_block5): Sequential(
    (0): Conv2d(64, 6, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (1): ReLU()
    (2): Conv2d(6, 6, kernel_size=(3, 3), stride=(1, 1), 
padding=(1, 1))
    (3): ReLU()
    (4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (fc): Sequential(
    (0): FlattenLayer()
    (1): Linear(in_features=3136, out_features=512, bias=True)
    (2): ReLU()
    (3): Dropout(p=0.5, inplace=False)
    (4): Linear(in_features=512, out_features=512, bias=True)
    (5): ReLU()
    (6): Dropout(p=0.5, inplace=False)
    (7): Linear(in_features=512, out_features=10, bias=True)
  )
)

NIN

1×1卷积层妙用！！！

xxx