【机器学习】GAN探究

本人主页

首先根据这个看一看，试着做一次https://zhuanlan.zhihu.com/p/117529144

然后是书上的生成动漫头像

最后是使用数据集的这个

https://pytorch.apachecn.org/docs/1.4/13.html

[toc]

小知识点

np.vstack()和np.hstack()

前者按垂直方向（行顺序）堆叠数组构成一个新的数组

In[3]:
import numpy as np

In[4]:
a = np.array([[1,2,3]])
a.shape
Out[4]:
(1, 3)

In [5]:
b = np.array([[4,5,6]])
b.shape
Out[5]:
(1, 3)

In [6]:
c = np.vstack((a,b)) # 将两个（1,3）形状的数组按垂直方向叠加
print(c)
c.shape # 输出形状为（2,3）
[[1 2 3]
 [4 5 6]]
Out[6]:
(2, 3)

In [7]:
a = np.array([[1],[2],[3]])
a.shape
Out[7]:
(3, 1)

In [9]:
b = np.array([[4],[5],[6]])
b.shape
Out[9]:
(3, 1)

In [10]:
c = np.vstack((a,b))  # 将两个（3,1）形状的数组按垂直方向叠加
print(c)
c.shape # 输出形状为（6,1）
[[1]
 [2]
 [3]
 [4]
 [5]
 [6]]
Out[10]:
(6, 1)

a=np.array([1,2,3])
print(np.vstack(a))
输出：
[[1]
 [2]
 [3]]

[:,np.newaxis]

和上面的用处一样，都是为了增加维度，向量变成矩阵，否则单独的数据向量是没法后面计算的。

np.random.seed(n)函数用于生成指定随机数。

把seed()中的参数比喻成“堆”；eg. seed(5)：表示第5堆种子。

seed()中的参数被设置了之后，np.random.seed()可以按顺序产生一组固定的数组，如果使用相同的seed()值，则每次生成的随机数都相同。如果不设置这个值，那么每次生成的随机数不同。但是，只在调用的时候seed()一下并不能使生成的随机数相同，需要每次调用都seed()一下，表示种子相同，从而生成的随机数相同。（你从同一堆里面按照相同方法取随机数，结果当然相同）

例1（只调用一次seed()，两次的产生随机数不同）

import numpy as np
np.random.seed(1)

L1 = np.random.randn(3, 3)
L2 = np.random.randn(3, 3)
print(L1)
print(L2)

结果

[[ 1.62434536 -0.61175641 -0.52817175]
 [-1.07296862  0.86540763 -2.3015387 ]
 [ 1.74481176 -0.7612069   0.3190391 ]]
 
[[-0.24937038  1.46210794 -2.06014071]
 [-0.3224172  -0.38405435  1.13376944]
 [-1.09989127 -0.17242821 -0.87785842]]

例2（调用两次seed()，两次产生的随机数相同）

import numpy as np

np.random.seed(1)
L1 = np.random.randn(3, 3)
np.random.seed(1)
L2 = np.random.randn(3, 3)
print(L1)
print(L2)

结果

[[ 1.62434536 -0.61175641 -0.52817175]
 [-1.07296862  0.86540763 -2.3015387 ]
 [ 1.74481176 -0.7612069   0.3190391 ]]
 
[[ 1.62434536 -0.61175641 -0.52817175]
 [-1.07296862  0.86540763 -2.3015387 ]
 [ 1.74481176 -0.7612069   0.3190391 ]]

查看tensor的shape

某个tensor已经得到了，比如使用a=torch.from_numpy()函数得到的。想看它的shape的时候，只能print(a.shape)，万万不可shape()，因为tensor没有shape()这个方法，只是一个属性。

细讲代码

以下讲解背景和代码参考**这个**，不再叙述

torch.manual_seed(1)
np.random.seed(1)#随机数种子，

LR_G=0.0001
LR_D=0.0001
BATCH_SIZE=64
N_IDEAS=5

ART_COMPONETS=15#输出的是一个15个点的函数取值
PAINT_POINTS=np.vstack([np.linspace(-1,1,ART_COMPONETS)])#此句vstack换为array依然可以。将-1~1分成15份

plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='upper bound')    #2*x^2 + 1
plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='lower bound')    # x^2
plt.legend(loc='upper right')           #标签位置
plt.show()

生成的数据应该在两条线之间的位置

插一句这里使用GAN的原理，因为我们是最终想要得到能够生成和给定数据一样类别分布的生成器。我们人为的把理想数据生成在两条线之间，然而神经网络并不知道分布是啥，它需要在不断对抗中自己学会。

理想数据生成器

随后，借用随机数种子，在两条线之间生成数据

def artist_work():
    a=np.random.uniform(1,2,size=BATCH_SIZE)[:,np.newaxis]
    paints = a * np.power(PAINT_POINTS,2) + (a-1)#a*x^2+a-1 (a~(1,2))
    paints = torch.from_numpy(paints).float()
    return paints	#是一个64×15的张量，并且在两条线之间，

给出批量样本特征为$X\in\R^{64\times15}$，注意所说的是批量、样本特征，批量指一批训练有64个样本（想想线性回归），15是每个样本15个特征

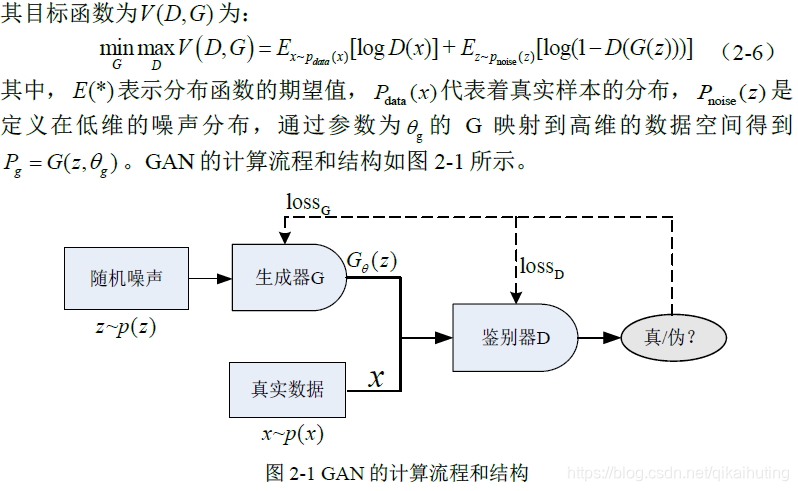
之所以需要理想数据呢，是因为我们需要真实数据给D网络来进行参照对比。

G网络和D网络

G = nn.Sequential(
    nn.Linear(N_IDEAS,128),#全连接层
    nn.ReLU(),
    nn.Linear(128,ART_COMPONETS)#生成器把特征空间的128数据生成15维的
)

（参考）G是生成网络，N_IDEAS是输入的二维张量的大小，128是输出的二维张量的大小，即输出的二维张量的形状为[batch_size，output_size]，当然，它也代表了该全连接层的神经元个数。
从输入输出的张量的shape角度来理解，相当于一个输入为[batch_size, in_features]的张量变换成了[batch_size, out_features]的输出张量。

D = nn.Sequential(
    nn.Linear(ART_COMPONETS,128),#别忘了ART_COMPONETS是我们产生随机数据的维度15
    nn.ReLU(),
    nn.Linear(128,1),		#输出1是为了sigmod
    nn.Sigmoid()            #因为对于D的评估应该是在[0-1]之间的数值，所以这里采用的是Sigmod激活
)
optimizer_G = torch.optim.Adam(G.parameters(),lr=LR_G)#实现Adma算法。lr是学习率，默认为0.001，G.parameters是G中的待优化参数
optimizer_D = torch.optim.Adam(D.parameters(),lr=LR_D)

开始训练

for step in range(10000):
    artist_painting=artist_work()#得到给D网络参考指导数据，64×15
    G_idea=torch.randn(BATCH_SIZE,N_IDEAS)#输入G的随机数，64×5
    G_paintings=G(G_idea)#G网络根据随机数生成结果 128×15

    pro_atrist0 = D(artist_painting)    #为D网络对于指导数据，评判后的输出结果，sigmod输出为0或者1
    pro_atrist1 = D(G_paintings)        #为D网络对于生成的数据，评判后的输出结果

    G_loss=-1/torch.mean(torch.log(1.-pro_artist1))
    D_loss=-torch.mean(torch.log(pro_artist0)+torch.log(1-pro_artist1))

    optimizer_D.zero_grad()
    D_loss.backward(retain_graph=True)

    optimizer_G.zero_grad()
    G_loss.backward(retain_graph=True)
    '''为什么retain_graph要设置为True，这是因为由于网络结构的复杂性，需要多次反向传播backward()积累同一个网络的grad，再进行一次前向传播forward()。而在我们的网络中，G和D虽然看上去是分别更新优化的，但是计算D的loss的时候，需要用到G网络得到的结果pro_artist1，因此不能着急step，要等两个网络都反向求导完了之后，再一起更新(forward/step())。
    '''
    optimizer_G.step()
    optimizer_D.step()

其中损失函数请看这里，还有这里

优化器与损失函数（极重要）

https://blog.csdn.net/liuweiyuxiang/article/details/84556275

https://blog.csdn.net/xiaoxifei/article/details/87797935

损失函数

在这里插入图片描述

对于损失函数的意义：

在这里插入图片描述

首先我们不要忘了，loss的来源是谁，其实就是鉴别器D对于两个来源的数据分别进行计算，最后sigmod得出的结果，分别是$D(x^{(i)})$和$D(G(z^{i}))$，x是真实数据，z是从随机数据中生成的假数据，而m是这些数据的个数，即batch size。先不看梯度符号，第一项即为判别器的损失函数，$logD(x^{(i)})$为判别器将真实数据判定为真的概率，$logD(1-(G(z^{(i)}))$为判别器将生成器生成的虚假数据，判定为真实数据的对立面——即将虚假数据仍判定为假的概率。

第二个式子为第一个式子的第二项，含义相同，只不过对于生成器应当最小化该项，生成器当然希望辨别器将虚假数据仍判定为假的概率越低越好，即将虚假数据误判定为真的概率越大越好，即最大化$logD(1-(G(z^{(i)}))$损失函数。所以二者相互提高或者减小自身的损失，以不断互相对抗。

我们有了Loss Function，在反向传播的时候，自然是向着梯度下降，让LF越来越小。对于第一项，LF越来越小，则两个判断正确的概率越来越大。对于第二项，则是把生成器的输出判断为假的概率越来越小，这样就也达到了对抗的目的！！！

优化器

在pytorch中，我们也无需自己实现随机梯度下降啊之类的算法，torch.optim模块提供了很多可使用的优化算法，比如SGD,Adam和RMSProP等，我们在代码中使用的就是Adam

optimizer_G=torch.optim.Adam(G.parameters(),lr=LR_G)
optimizer_D=torch.optim.Adam(D.parameters(),lr=LR_D)
'''用这一句其实就可以控制子网络中的学习率了。如果使用optimizer.param_group模块，还可以新建优化器，使得学习率不是固定为一个常数。但是Adam是基于动量的优化器，在训练过程中的变化的话会丢失动量等信息，可能会造成损失函数出现震荡等
'''

# print(G,D)
print(optimizer_G)
Adam (
Parameter Group 0
    amsgrad: False
    betas: (0.9, 0.999)
    eps: 1e-08
    lr: 0.0001
    weight_decay: 0
)

在最后的训练代码中，最关键的还是损失函数的的backward()和优化器的step()，他们又具体在干什么呢？

我们不妨先看另一个例子(《D2L》3.3.7)

num_epochs = 3
for epoch in range(1, num_epochs + 1):
	for X, y in data_iter:
		output = net(X)
		l = loss(output, y.view(-1, 1))
		optimizer.zero_grad() 
		l.backward()
		optimizer.step()
	print('epoch %d, loss: %f' % (epoch, l.item()))

定义了损失函数（从net的输出$\hat{y}$和实际参考数据y中得到）

–>优化器梯度清零，不想要梯度累计

–>损失函数反向传播

–>优化器进行迭代一次（其中优化器的step()对整批的梯度求平均了）

反向传播参考

反向求导和权重更新是两个过程，这也就是为什么有损失函数的反向传播了还要优化器，反向求导，是更新梯度的过程，那根据什么来更新梯度呢，就是根据你的损失函数（想想李宏毅的那个山坡图）。我们在更新了梯度之后，就

反向求导和权重更新之所以能够联系起来，是因为损失函数进行backward()的过程中，是将net的参数params已经更新了——是那个tensor的梯度已经进行了更新。而后面权重更新的时候，优化器也是对那个网络，那个tensor进行的操作，因此自然能够练习在一起。这样一次发向传播，一次正向传播，就能够达到了目的

为什么是按照loss function的梯度进行下降？因为你的目标是让Loss Function最小化啊！！！别忘了

至此，本例子的代码和牵扯到的原理已经讲清楚——2021.7.31（成都夏天热死了）